The Shortcut in Differentiating the Backwards Pass in Batch Normalization

Introduction

This read may be a little ridiculous because instead of substituting partials as needed when working through the math, I do everything at once in the most expanded form. I link an alternative, maybe more interpretable, blog down below in the conclusion. This read is not very suitable for smaller screens.

The image below defines "whitening". An application to a batch of inputs with the goal to reduce the internal covariate shift. This procedure occurs during the forward pass. In order to preserve training, the backward pass must also be defined. Similarly to how the gradient of the sigmoid function simplifies to (1−σ(x))(σ(x)), the gradient for batch normalization can also undergo a similar process to promote computational efficiency (link to paper).

During training, the chain rule is shown to backpropagate through the batch normalization transformation (page 4 of the paper). The code block was my implementation.

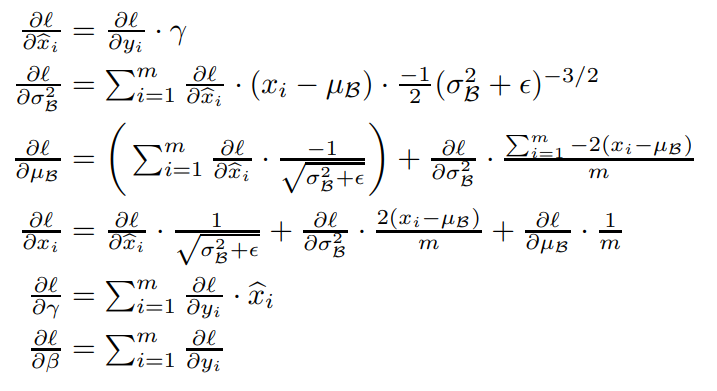
   @staticmethod
   def backward(dout, cache):

      # dout: upstream gradient
      # cache: cache of intermediate variables to construct local gradient

      dx, dgamma, dbeta = None, None, None
      x, xhat, bMean, bVar, eps, gamma, beta = cache
      N, D = dout.shape

      dxhat = dout * gamma
      dbVar1 = torch.sum(dxhat * (x - bMean), 0)
      dbVar2 = ((-1/2)*((bVar + eps))**(-3/2))
      dbVar =  dbVar1 * dbVar2
      dMean = torch.sum(dxhat * -1/torch.sqrt(bVar + eps), 0) + dbVar * (torch.sum(-2*(x - bMean), 0))/ N
      x1 = dxhat * (1/torch.sqrt(bVar + eps)) 
      x2 = dbVar * (2 * (x - bMean)/ N)
      x3 = dMean * (1 / N)
      # Standard dl/dx composed of 373 characters
      dx = x1 + x2 + x3

      dgamma = torch.sum(dout * xhat, 0)
      dbeta = torch.sum(dout, 0)

      return dx, dgamma, dbeta

Total Derivative Representation

Now lets find a better way to pass backwards through batch normalization using the derivative. Above is a "full" representation of the total derivative of $\frac{\partial{\ell}}{\partial{x_i}}$. I wrote the "full" (as opposed to the truly full) representation first for ease of understanding. The third term in the second summand: $\frac{\mathrm{d}{\hat{x_i}}}{\mathrm{d}{\mu_\beta}}$, can be further decomposed because $\mu_\beta$ is an argument of $\hat{x_i}$ and the intermediate variable $\sigma^2_\beta$. It looks like:

The full represetation without quotes:

Integrate Summations

The downstream gradient will always match the dimensionality of whatever you're differentiating with respect to. This means you have to sum over the elements if the upstream is of a higher rank than your downstream. For batch normalization, the metaphorical local jacobian, which you multiply by the upstream, will instead be a conglomeration of intermediary functions. Below I integrate summations into the total derivative to reduce dimensionality as the betas all reference a scalar value for each feature of the entire batch. (aka: Derivative of rank 2 tensor wrt rank 1 tensor goes through summation to produce a rank 1 tensor which matches dimensionality of what we're differentiating wrt to).

For clarity, you can rewrite redundant partials into a generalized form: $\frac{\partial{\ell}}{\partial{y_i}} \cdot \frac{\partial{y_i}}{\partial{\hat{x_i}}} = \frac{\partial{\ell}}{\partial{\hat{x_i}}}$

Solving the Partials

Solve for all of the partials shown above. This is the easiest part. The upstream gradient defined immediately below is automatically provided to the function when backpropagating. Special consideration to $\frac{\partial{\sigma^2_\beta}}{\partial{\mu_\beta}}$ and $\frac{\partial{\sigma^2_\beta}}{\partial{x_i}}$ as there are summations in their functions. The sigma notation in $\frac{\partial{\sigma^2_\beta}}{\partial{x_i}}$ does not carry over because we are differentiating wrt a vector.

Substitute in Partials & Simplify

Every partial is evaluated. Substitute in everything except dout to the template from step 1. Leaving it's partial provides headspace for knowing what some of the summations will be operating on. Note that I've changed the nested summations index to k. It will initially look more confusing, but simplifies well :). (be careful to consider equations overflowing to the next line)

1

I'm going to work on the middle summand first. Rewrite $(\sigma^2_\beta+\epsilon)^{-3/2}$ as $(\sigma^2_\beta+\epsilon)^{-1/2}\frac{1}{\sqrt{\sigma^2_\beta+\epsilon}}\frac{1}{\sqrt{\sigma^2_\beta+\epsilon}}$. I will also slowly be removing the dot notation where multiplication is obvious.

2

Further simplify the nested summation $\frac{-2}{m}\sum_{i=1}^{m}(x_i-\mu_\beta)$ by distributing the sigma to it's terms.

3

4

5

6

On equation 4 after distributing the sums, the values both simplify to the expectation over the batch $\mu_\beta$. I do not break down $\frac{m\mu_\beta}{m}$ immediately as I did for $\frac{1}{m}\sum_{i=1}^{m}x_i$ for understanding; $\mu_\beta$ is being summed up m times then divided by m. The difference in the parenthesis evaluates to 0 and then the labor of "10 steps backwards 11 steps forward" is shown. Equation 6 drops everything multiplied by zero and cleans up some of the left hand side of the equation.

Now we begin simplifying right-most summand. Before we factor out constants, we combine a couple of the terms (money step). For ease of understanding, I've also put it in equation 6, but I change the index of the right-most product from i to k. This is because it has to be treated as a constant to the summation.

7

Factor out constants

8

The reason I mentioned combining terms in equation 7 was the money step is because the term $\frac{x_i-\mu_\beta}{\sqrt{\sigma^2_\beta+\epsilon}}$ is equal to the normalization step $\hat{x_i}$ in the backward pass of batch normalization. I substitute in $\hat{x_i}$, which will be a parameter passed to our backward pass function from the forward pass stored in the cache (shown later), I change the square root representation to make factoring later more amenable, and I clean up stray terms.

9

Some final cleaning by factoring our similarities from the 3 terms.

10

Below is a codeblock implemented with equation 10. With a 276 character difference, the shortcut performs a backwards pass much faster than the original implementation.

   @staticmethod
   def backward_alt(dout, cache):

      # dout: upstream gradient
      # cache: cache of intermediate variables to construct local gradient

      dx, dgamma, dbeta = None, None, None
      x, xhat, bMean, bVar, eps, gamma, beta = cache
      N, D = dout.shape

      dbeta = torch.sum(dout, 0)
      dgamma = torch.sum(dout * xhat, 0)
      # Optimized dl/dx composed of 97 characters
      dx = gamma/torch.sqrt(bVar + eps) * (dout - torch.sum(dout, 0)/N - xhat/N * torch.sum(dout * xhat, 0))

      return dx, dgamma, dbeta
   # >>> ~3-10x faster than backward()

Thoughts

I made a joke to it earlier by stating "10 steps backwards 11 steps forward", but this exercise really embodied that expression. Originally I had trouble with understanding where summations belonged so there were a handful of errors by the time I got to step 3 causing me to scrap a chunk of the work. I found out that defining them rigidly in my current step 1 helped tremendously to save brain space. I also realized that you can "interweave" total derivatives with partials (prior to step 1) - doubt I'll be doing that again. If you're looking for a more readable interpretation of this exercise, check out this blog post. The author substitutes in the partials as needed as opposed to doing it all at once as I did. The reason why I did it all at once was a combination of solidifying understanding, making explanations unambiguous, and having fun. Some of the simplifications in equations 1-10 are inefficient for the same reasons. If anybody struggles with concepts affiliated to total/partial derivatives wrt vectors this is a good exercise to do. Feel free to ping me if you see any errors or have any suggestions/considerations :).

Ryan Lin