Transformers Deconstructed and Explained

Introduction

I'm going to explain, hopefully thoroughly enough, the mechanisms present in Transformers. I reference the accompanied paper to the network Attention Is All You Need a couple times throughout this read. Feel free to click around through the contents displayed above to read more about a particular section and the affiliated code. Similarly to other articles I've written, all code uses the PyTorch framework.

It is mentioned in the opening of the Attention is All You Need that the Transformer model was introduced to ameliorate and "push the boundaries of recurrent language models and encoder-decoder architectures". While this was certainly true back when Transformers were new, it is worth mentioning that the impact of Transformers has broached well into other domains of machine learning. Visual Transformers and Swin Transformers are good examples. Although Computer Vision already has sequential tasks such as image captioning, those linked papers use the attention mechanism to process the image data itself, which is not inherently sequential.

Transformers can be laid out in the following:

Transformer

   - Embedding 
   - Positional Encoding

   - Encoder
      - Encoder Block
         - MultiHeaded Attention
            Self Attention
               Scaled Dot Product Attn
         - Feed Forward Block
            Linear -> Act -> Linear
         - Normalization
         - Residual Connections
   
   - Decoder
      - Decoder Block
         - Multi Headed Attention
            Self Attention
               Scaled Dot Product Attn
         - Masked Multi Headed Attention
            Self Attention
               Scaled Dot Product Attn
         - Feed Forward Block
            Linear -> Act -> Linear
         - Normalization
         - Residual Connections

By decomposing Transformers as such, it becomes easier to see the constituent parts. For example, you can see there's a lot of importance on Scaled dot product attention because it is used heavily throughout the entire model. Every attention mechanism, whether it be masked, multiheaded, or cross employs SDP attention. Below is the visualization of a Transformer from the orginitating paper (linked above). It is easy to see features such as the information flow throughout the network and finer detail such as how each attention block takes in three arguments (queries, keys, values) and skip connections to aid gradient flow.

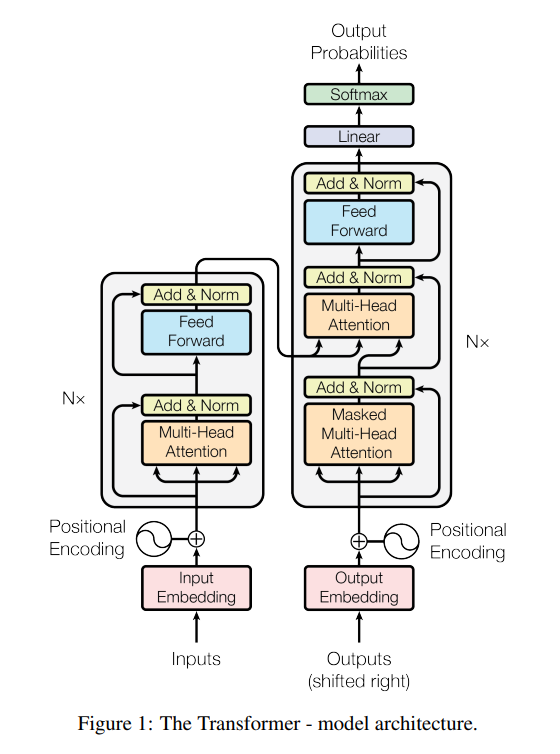
Transformer layout from "Attention is All You Need"

Preparation

Before the sequence inputs can be fed into the encoder and decoder, they must be tokenized, pass go through an embedding layer, and then have positional encoding added to them. Tokenization is the process of converting a sequence, for example something that can be human interpretable, into a sequence of tokens represented as integers. For the embedding layer, I am going to be using nn.Embedding available through PyTorch. Positional encoding is defined below.

def positionalEncoding(K, E):
   """
   k: sequence dimension
   e: embedding dimension

   y: shape (1, K, E) tensor
   """

   y = torch.zeros(K, E)

   p = torch.arange(0, K).unsqueeze(1) # Make column vector
   i = torch.arange(0, E).unsqueeze(0) # Make row vector
   a = torch.floor(2*i / E)

   y[:, 0::2] = torch.sin(p / torch.pow(10000, a[0, 0::2]))
   y[:, 1::2] = torch.cos(p / torch.pow(10000, a[0, 1::2]))

   return y.unsqueeze(0)

Scaled Dot Product Attention

Scaled dot product attention takes three arguments as input: queries, keys, and values. These inputs originate from the same tensor and each go through the same shape transformation except with unique weights. More is discussed specifically about this in the Self Attention class section.

Supplied with our Q, K, and V (queries/keys/values respectively), scaled dot product attention on a single element from the batch will look like:

where $K \in \mathbb{R}^{k \times e}, Q \in \mathbb{R}^{k \times e}, V \in \mathbb{R}^{k \times e}$.

Fortunately in code, we can perform batch operations to calculate the attention values all at once. I encourage looking at the PyTorch SDP Attention implementation found here (You may need to ctrl+f "scaled_dot_product_attention"). I will sprinkle in the corresponding PyTorch code at every now and then.

def scaled_dot_product_attention(q: Tensor, k: Tensor, v: Tensor, mask: Tensor = None):
   """
   q: shape (B, K, E) where B is batch size, K is sequence length,
      and E is the embedding dimension
   k: shape (B, K, E) where B is batch size, K is sequence length,
      and E is the embedding dimension
   v: shape (B, K, E) where B is batch size, K is sequence length,
      and E is the embedding dimension
   mask: shape (B, K, K) where B is batch size and K is sequence length

   y: shape (B, K, E) where B is batch size, K is sequence length,
      and E is the embedding dimension
   softmax_weights: (B, K, K) where B is batch size and K is sequence length
   """
   B, K, E = q.shape

   # Similarity matrix 
   e = torch.bmm(query, key.transpose(1, 2)) # (B, K, K)

   # For Multi Headed Attention
   if mask is Not None:
      e = e.masked_fill_(mask.to(e.device), -1e9)
      # e[mask] = -1e9

   # Attention matrix
   softmax_weights = (e / E**(1/2)).softmax(dim=-1)

   # Second batch mat-mul of weights_softmax with values
   y = torch.bmm(softmax_weights, v)
   
   return y, softmax_weights # (B, K, E), (B, K, K)

Attention Implementation

We can now construct the classes that house SDP Attention. It's worth mentioning that there are different ways how you can code the model (Pytorch's Transformer). The way shown here will certainly have its idiosyncrasies, so my goal is to really convey the main mechanisms present in all of these variations. I will occasionally toss in different characteristics of other Transformer models.

class SelfAttention(nn.Module):
   def __init__(self, dim_in: int, dim_q: int, dim_v: int):
      super().__init__()
      """
      dim_in: input dimension size of query, key, and value
      dim_q: output dimension size of query and key vectors
      dim_v: output dimension size of value vector
      """
      
      self.q = nn.Linear(dim_in, dim_q)
      self.k = nn.Linear(dim_in, dim_q)
      self.v = nn.Linear(dim_in, dim_v)
      self.softmax_weights = None

      # Weights initialized to different distribution using self.q as ex.
      # self.c = (6/(dim_in + dim_q))**(1/2)
      # torch.nn.init.uniform(self.q.weight, -self.c, self.c)
      #
      # torch.nn.init.xavier_uniform_(self.q.weight)
      
   def forward(self, q: Tensor, k: Tensor, v: Tensor, mask: Tensor = None):
      """
      q: shape (B, K, E) tensor where B is batch size, K is sequence length,
         and E is the embedding dimension
      k: shape (B, K, E) tensor where B is batch size, K is sequence length,
         and E is the embedding dimension
      v: shape (B, K, E) tensor where B is batch size, K is sequence length,
         and E is the embedding dimension
      mask: shape (B, K, K) boolean tensor where B is batch size and K is
      sequence length

      y: shape (B, K, dim_v) tensor where B is batch size and K is sequence length
      """

      k = self.k(k) # (B, K, dim_q)
      q = self.q(q) # (B, K, dim_q)
      v = self.v(v) # (B, K, dim_v)
      
      y, self.softmax_weights = scaled_dot_product_attention(k, q, v, mask)
      
      return y # (B, K, dim_v)

class MultiHeadAttention(nn.Module):
   def __init__(self, num_heads: int, dim_in: int, dim_out: int):
      super().__init__()
      """
      num_heads: number of heads
      dim_in: input dimension size for the query, key, and value
      dim_out: output dimension for each SA block
      """
   
      self.heads = \
         torch.nn.ModuleList([SelfAttention(dim_in, dim_out, dim_out) for i in range(num_heads)])
      # self.linear adopts same concept for weight initialization from SelfAttention class
      self.linear = nn.Linear(dim_out * num_heads, dim_in)
   
   def forward(self, q: Tensor, k: Tensor, v: Tensor, mask: Tensor = None):
      """
      q: shape (B, K, E) tensor where B is batch size, K is sequence length,
         and E is the embedding dimension
      k: shape (B, K, E) tensor where B is batch size, K is sequence length,
         and E is the embedding dimension
      v: shape (B, K, E) tensor where B is batch size, K is sequence length,
         and E is the embedding dimension
      mask: shape (B, K, K) boolean tensor where B is batch size and K is
      sequence length

      y: shape (B, K, dim_in) tensor where B is batch size and K is sequence length
      """

      output_list = []
      
      for m in self.heads:
         y = m(q, k, v, mask) # (B, K, dim_out)
         output_list.append(y)
         
      concat = torch.cat(output_list, dim=-1) # (B, K, num_heads * dim_out)
      y = self.linear(concat) 
      
      return y # (B, K, dim_in)

def get_subsequent_mask(seq)
   """
   seq: shape (B, K) tensor where B is batch size and K is sequence length

   mask: shape (B, K, K) boolean tensor where B is batch size and K is
      sequence length
   """
   # Pytorch's implementation
   # https://pytorch.org/docs/stable/_modules/torch/nn/modules/transformer.html#Transformer.forward
   mask = torch.triu(torch.full( \
      (seq.shape[1], seq.shape[1]), float('-inf'), dtype=torch.bool), diagonal=1)
   mask = mask.repeat((seq.shape[0], 1, 1))

   # Alternative not using Pytorch source code
   # mask = torch.ones((seq.shape[0], seq.shape[1], seq.shape[1]), dtype=torch.bool)
   # for n in range(seq.shape[0]):
   #     for k in range(seq.shape[1]):
   #         mask[n, k, :k+1] = 0
   
   return mask

Feed Forward Network

A standard feed forward network composed of a linear -> ReLU -> linear tranformation is used at the end of every block. The first linear layer transforms the input into dimension $d_{ff}$, which will be a provided hyperparameter - Attention Is All You Need uses 2048. The second linear layer reforms that $d_{ff}$ tensor back to a $d_{in}$ dimensional tensor, another provided hyperparameter. Retaining original shape is important as generally the feed forward nets will need to feed into another encoder or decoder block.

class FeedForward(nn.Module):
   def __init__(self, inp_dim: int, hidden_dim_forward: int):
      super().__init__()
      """
      inp_dim: embedding dimension
      hidden_dim_forward: hidden dimension for linear layers
      """
      
      self.mlp = nn.Sequential(
            nn.Linear(inp_dim, hidden_dim_feedforward),
            nn.ReLU(),
            nn.Linear(hidden_dim_feedforward, inp_dim)
      )
      
      # nn.Linear weight initialization adopts same concept as SelfAttention class
      # self.c = (6/(inp_dim + hidden_dim_forward))**(1/2)
      # torch.nn.init.uniform(self.q.weight, -self.c, self.c)
      #
      # torch.nn.init.xavier_uniform_(self.q.weight)
      
   def forward(self, x):
      """
      x: shape (B, K, E) tensor where B is batch size, K is sequence length,
         and E is the embedding dimension
      
      y: shape (B, K, E) tensor where B is batch size, K is sequence length,
         and E is the embedding dimension
      """
      y = self.mlp(x)
      
      return y

Blocks

We can now build both the encoder and decoder blocks. All of the constituent pieces to the blocks have been built and we are ready to instantiate everything inside a EncoderBlock class and DecoderBlock class. Once we've finished creating the blocks, we then need to wrap them one more time in an Encoder and Decoder class respectively. This is to modularize them so we can have N layers for our encoder and decoder stack. Following along using the image of the Transformer at the top may help. Normalization, residual, and regularization techniques will also be pointed out in the forward passes of each block here.

class EncoderBlock(nn.Module):
   def __init__(self, num_heads: int, emb_dim: int, feedforward_dim: int, dropout: float)
      super().__init__()
      """
      Hyperparameters defined in Transformer class section
      """
      
      self.multihead = MultiHeadAttention(num_heads, emb_dim, emb_dim // num_heads)
      self.layernorm = nn.LayerNorm(emb_dim, eps=1e-10)
      self.dropout = nn.Dropout(dropout)
      self.feedforward = FeedForward(emb_dim, feedforward_dim)
   
   def forward(self, x):
      """
      x: shape (B, K, E) tensor where B is batch size, K is sequence length,
         and E is the embedding dimension
         
      y: shape (B, K, E) tensor where B is batch size, K is sequence length,
         and E is the embedding dimension
      """

      y = self.layernorm(self.multihead(x, x, x) + x)
      y = self.dropout(y) # (B, K, E)
      y = self.layernorm(self.feedforward(y) + y)
      y = self.dropout(y) # (B, K, E)
      
      return y

class DecoderBlock(nn.Module):
   def __init__(self, num_heads: int, emb_dim: int, feedforward_dim: int, dropout: float)
      super().__init__()
      """
      Hyperparameters defined in Transformer class section
      """

      self.self_attention = MultiHeadAttention(num_heads, emb_dim, emb_dim // num_heads)
      self.cross_attention = MultiHeadAttention(num_heads, emb_dim, emb_dim // num_heads)
      self.feed_forward = FeedForward(emb_dim, feedforward_dim)
      self.layernorm = nn.LayerNorm(emb_dim, eps=1e-10)
      self.dropout = nn.Dropout(dropout)
      
   def forward(self, dec_inp: Tensor, enc_out: Tensor, mask: Tensor = None):
      """
      dec_inp: shape (B, K, E) tensor where B is batch size, K is sequence length,
         and E is the embedding dimension
      enc_out: shape (B, K, E) tensor where B is batch size, K is sequence length,
         and E is the embedding dimension
      mask: shape (B, K, K) boolean tensor

      y: shape (B, K, E) tensor
      """
      
      y = self.layernorm(self.self_attention(dec_inp, dec_inp, dec_inp, mask) + dec_inp)
      y = self.dropout(y) # (B, K, E)

      y = self.layernorm(self.cross_attention(y, enc_out, enc_out) + y)
      y = self.dropout(y) # (B, K, E)

      y = self.layernorm(self.feed_forward(y) + y)
      y = self.dropout(y) # (B, K, E)
      
      return y

Encoder & Decoder Layers

As mentioned in the blocks section, let us now wrap everything in an Encoder and Decoder class. This is so we can easily define a model with N encoder and decoder layers. The only thing I'd like to point out here is the final linear transformation present in the Decoder class. After all we need to transform the embedding dimension of our tensor from the embedding size back to the size of possible classifications for a sequence element.

class Encoder(nn.Module):
   def __init__(self, num_heads: int, emb_dim: int, feedforward_dim: int, num_layers: int, dropout: float):
      super().__init__()   
      """
      Hyperparameters defined in Transformer class section
      """

      self.layers = nn.ModuleList(
         [EncoderBlock(num_heads, emb_dim, feedforward_dim, dropout) for _ in range(num_layers]
      )
   
   def forward(self, src_seq: Tensor):
      """
      (input & output)
      src_seq: shape (B, K, E) tensor where B is batch size, K is sequence length,
         and E is the embedding dimension
      """
      for layer in self.layers:
         src_seq = layer(srq_seq) 
      
      return src_seq

class Decoder(nn.Module):
   def __init__(
      self, num_heads: int, emb_dim: int, feedforward_dim: int, num_layers: int, dropout: float, class_len: int,
   ):
      super().__init__()'
      """
      Hyperparameters defined in Transformer class section
      """

      self.layers = nn.ModuleList(
         [DecoderBlock(num_heads, emb_dim, feedforward_dim, dropout) for _ in range(num_layers)]
      )
      self.proj_to_class = nn.Linear(emb_dim, class_len)

      # Weight initialization similar to Self Attention
      # c = (6 / (emb_dim + class_len)) ** 0.5
      # nn.init.uniform_(self.proj_to_class.weight, -c, c)

   def forward(self, target_seq: Tensor, enc_out: Tensor, mask: Tensor):
      """
      The encoder sequence length K does not have to equal the decoder sequence length K!
      
      target_seq: shape (B, K, E) tensor where B is batch size, K is sequence length,
         and E is the embedding dimension
      target_seq: shape (B, K, E) tensor where B is batch size, K is sequence length,
         and E is the embedding dimension
      mask: shape (B, K, K) boolean tensor

      out = shape (B, K, class_len) tensor where B is batch size and K is sequence length,
         and class_len is the total possible classifications
      """

      out = target_seq.clone() # (B, K, E)
      
      for layer in self.layers:
         out = layer(out, enc_out, mask) # (B, K, E)

      out = self.proj_to_class(out) # (B, K, class_len)
      return out

Transformer

The Transformer model can finally be put together. Everything up to line 50 should look normal. In the constructor we instantiate the required classes with the according hyperparameters. In the forward pass, we pass both the tokenized enc_seq and trg_seq through nn.Embedding and then add their positional encodings with positionalEncoding. The results src_inp and trg_inp are then fed to the encoder and decoder respectively where the decoder will also take as input the output from the encoder to be used in the cross attention sublayer and a mask for the masked multi headed attention sublayer.

The reshaping at the end, on line 51, is such that the loss function takes in an appropiately sized input outputted from the Transformer. I usually use cross entropy, in which case the prediction is shape (B * K, class_len) and the ground truth is shape (B * K). The prediction variable houses the unnormalized scores (hence not softmaxing as shown in the Transformer image) and the ground truth variable houses the corresponding ground truth indices for each element of each sequence of every batch.

class Transformer(nn.Module):
   def __init__(
      self,
      num_heads: int,
      emb_dim: int,
      feedforward_dim: int,
      dropout: float,
      num_enc_layers: int,
      num_dec_layers: int,
      class_len: int
   ):
      """
      num_heads: number of heads
      emb_dim: embedding dimension
      feedforward_dim: feed forward dimension
      dropout: dropout probability
      num_enc_layers: number of encoder blocks
      num_dec_layers: number of decoder blocks
      class_len: total possible classifications for a sequence element
      """

      super().__init__()
        
      self.emb_layer = nn.Embedding(class_len, emb_dim)
      self.encoder = Encoder(num_heads, emb_dim, feedforward_dim, num_enc_layers, dropout)
      self.decoder = Decoder(num_heads, emb_dim, feedforward_dim, num_dec_layers, dropout)
      
   def forward(self, src_seq, trg_seq):
      """
      The encoder sequence length K does not have to equal the decoder sequence length K!
      
      src_seq: shape (B, K) tensor where B is batch size and K is sequence length
      trg_seq: shape (B, K) tensor where B is batch size and K is sequence length

      dec_out: shape (B * K, class_len) where class_len possible classifications
         for sequence element
      """

      src_emb = self.emb_layer(src_seq) # (B, K, E)
      src_inp = positionalEncoding(src_emb.shape[1], src_emb.shape[2]) + src_emb
      # Above: src_inp = (1, K, E) + (B, K, E)

      trg_emb = self.emb_layer(trg_seq) # (B, K, E)
      trg_inp = positionalEncoding(trg_emb.shape[1], trg_emb.shape[2]) + trg_emb
      # Above: src_inp = (1, K, E) + (B, K, E)

      mask = get_subsequent_mask(trg_seq) # (B, K, K)
      y = self.encoder(src_inp) # (B, K, E)
      dec_out = self.decoder(trg_inp, y, mask) # (B, K, class_len)

      dec_out = dec_out.view(-1, dec_out.size(2)) # (B * K, class_len)
      return dec_out

Thoughts

I *think* Transformers are the architecture I've spent the longest time reading about. In mid 2021, I was listening in on a discussion where different people gave their reponse to the question "what big changes do you expect to happen in ML?". One of the speakers was very confident that Transformers were going to take over industries as the flagship architecture. Not speaking to the creedence of that statement, the only thing I was made curious about were Transformers themselves. At the time, not only was I very unfamiliar with them, but I did not even know about Recurrent Networks. I remember reading about Transformers the following day, specifically the Attention Is All You Need paper, and feeling as if I had skipped a couple steps.

They're a pretty cool architecture though, no? The attention mechanism and all of its variations have introduced, for me at least, very unique ways you can go about manipulating information. And when arranged appropiately to constitute a single Transformer network, the strengths are very evident. The weaknesses are there too, however since one of its biggest is tied to hardware capability, I am a little forgiving.

I wanted to remain impartial to that one person who said Transformers are taking over every industry, but there has been some retaliation in favor of CNNs.

Ryan